Treatment vs. Experimental design - what is the difference?
1) Intro
A study design is comprised of two components:
- Treatment design
- Experimental design
The distinction between these two design components is not always clear, and commonly students are unsure they both exist altogether.
Below, I explain their differences, the objectives of each, and demonstrate an applied agronomic example.
2) Treatment design
Treatment design is the part of the study design related to what treatments you need to answer your hypothesis/objectives, and how they are related to one another.
For example, let’s say my objective is to determine the amount of potassium (K) and nitrogen (N) fertilizer that optimizes corn yield.
Let’s stop for a second and think about it.
If I want to find the optimum amount of an input, I really need to treat the crop with different levels of that input so I can estimate at which level the yield response is maximized.
Since we have two inputs (K and N), we need to do that for both of them.
Also, it may be that K and N interact in affecting corn yield, so we are interested in this effect too.
We have two treatment factors (K and N), and now let’s decide on their levels:
- K fertilizer: 0, 30, 60 kg K/ha
- N fertilizer: 0, 100, 200 kg N/ha.
Treatment factors: K and N fertilizer
Treatment levels: the rates chosen within the treatment factors (e.g., 0, 30, 60 kg K/ha)
Now, since we are interested in how K and N interact, we need to have in our treatment design all the combinations between K and N fertilizer levels. That leaves us with 3 K levels x 3 N levels = 9 total treatment combinations.
In other words, we need all the above 9 treatments to find the joint optimum K and N fertilizer rates that optimize corn yield.
With all this, our treatment design would be a crossed two-way factorial with 3 levels of K and 3 levels of N.
Note that our treatment factors are crossed, meaning that both K and N are at the same hierarchical level in the treatment design.
In contrast, treatment factors can also be nested, where the levels of one treatment factor are allocated within the levels of the other. Split-plot is an example where treatment factors are nested, meaning that one factor is at a higher hierarchy than the other (this is subject of a future post).
Now, notice that the treatment design has only addressed our objectives.
So what is the use of the experimental design?
3) Experimental design
Experimental design is the part of the study design related to how your treatments are assigned to the experimental units.
The decision of which experimental design to use should be guided by two factors:
- Homogeneity of experimental material
- Limitations such as funds, space in an incubator, size of the benches, size of a field.
Two of the most common experimental designs in agriculture are
- Completely randomized design (CRD)
- Randomized complete-block design (RCBD)
Continuing with our example of K and N levels, let’s assume that we would like to have 4 replications. That brings us to 9 treatments x 4 replications = 36 experimental units. The question that follows then is
“Do I have enough homogeneous experimental material to accommodate all 36 experimental units?”.
3.1) Homogeneous Experimental Material
If the answer is Yes, then you can use CRD as the experimental design, and treatments will be randomized to the entire area (no restrictions in randomization).
In the graph below, all treatments (1 through 9) were randomly assigned to any plot in the study area.
Here, treatment 1 and its replicates are highlighted.
Note how, due to the unrestricted randomization, treatment 1 appears twice in the first column, and does not appear on the third column. The same happened with other treatments.
Because the experimental material is homogeneous (same soil texture class), this should not be an issue when estimating treatment means and performing comparisons.
3.2) Heterogeneous Experimental Material
If the answer is No, then you should consider what types of limitation you have and which experimental design can be used.
Let’s say we answered No in our example. We have enough area to allocate 36 plots on the field, but we know that the area has heterogeneity in soil texture, a feature that likely impacts corn yield.
If we were to continue using a CRD, here’s what it would look like:
Note that following the same unrestricted randomization process, now treatment 1 appears 3 times under a darker soil texture, and only 1 time under a light soil texture. This happens for many treatments.
Suppose that dark soil texture has a positive effect on corn yield, and light soil texture has a negative effect.
In this case, using a CRD as in the example above, treatment 1 would likely have an average yield that is overestimated due to the unbalanced number of reps in each soil texture class.
This has a negative effect on both treatment means (biased) and on the analysis standard error (inflated), which makes treatment comparisons unfair and inaccurate (more difficult to detect real differences).
But, we can fix this by choosing an appropriate experimental design!
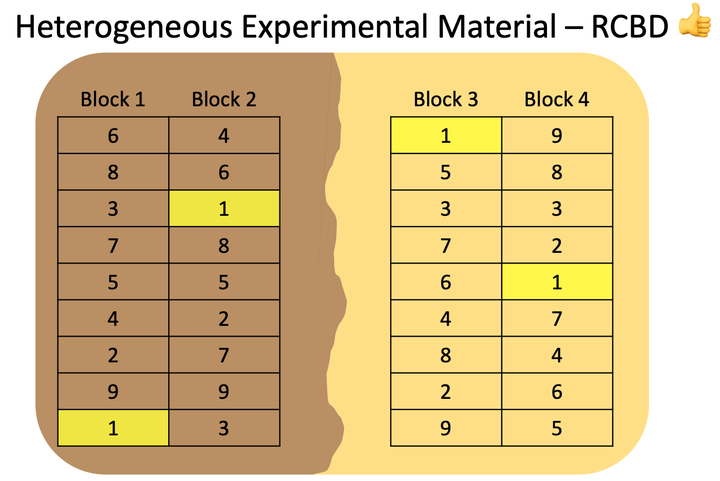
For that, we could use an RCBD, where blocks will be entirely confined within a given soil texture class.
Note how each treatment appears once and only once in every block. Now, the increased variability in corn yield caused by soil texture (experimental material heterogeneity) will be confined to the block effect, and thus can be properly dissected and not affect our inference on the treatment design variables.
There are other experimental designs that account for increasingly complicated limitations in experimental material.
Some of these include latin square, balanced incomplete block, partially confounded factorial, cyclic, lattice, supersaturated, response surface, and other designs.
4) Summary
Treatment design: addresses research question(s).
Experimental design: addresses lack of homogeneity and/or limitations (funds, size, etc.) of experimental material.
The proper choice of experimental design will allow for unbiased and accurate treatment comparisons.
Cheers,
Leo.
